Related Publications
-
On Bundle Adjustment for Multiview Point Cloud Registration
Huaiyang Huang, Yuxiang Sun, Jin Wu, Jianhao Jiao and
4 more authors.
IEEE Robotics and Automation Letters (RA-L), 2021
@article{huang2021bundle,
title={On Bundle Adjustment for Multiview Point Cloud Registration},
author={Huang, Huaiyang and Sun, Yuxiang and Wu, Jin and Jiao, Jianhao and Hu, Xiangcheng and Zheng, Linwei and Wang, Lujia and Liu, Ming},
journal={IEEE Robotics and Automation Letters},
volume={6},
number={4},
pages={8269--8276},
year={2021},
publisher={IEEE}
}
Abstract
Multiview registration is used to estimate Rigid Body Transformations (RBTs) from multiple frames
and reconstruct a scene with corresponding scans. Despite the success of pairwise registration and
pose synchronization, the concept of Bundle Adjustment (BA) has been proven to better maintain
global consistency. So in this work, we make the multiview point-cloud registration more tractable
from a different perspective in resolving range-based BA. Based on this analysis, we propose an
objective function that takes both measurement noises and computational cost into account. For the
feature parameter update, instead of calculating the global distribution parameters from the raw
measurements, we aggregate the local distributions upon the pose update at each iteration. The
computational cost of feature update is then only dependent on the number of scans. Finally, we
develop a multiview registration system using voxel-based quantization that can be applied in
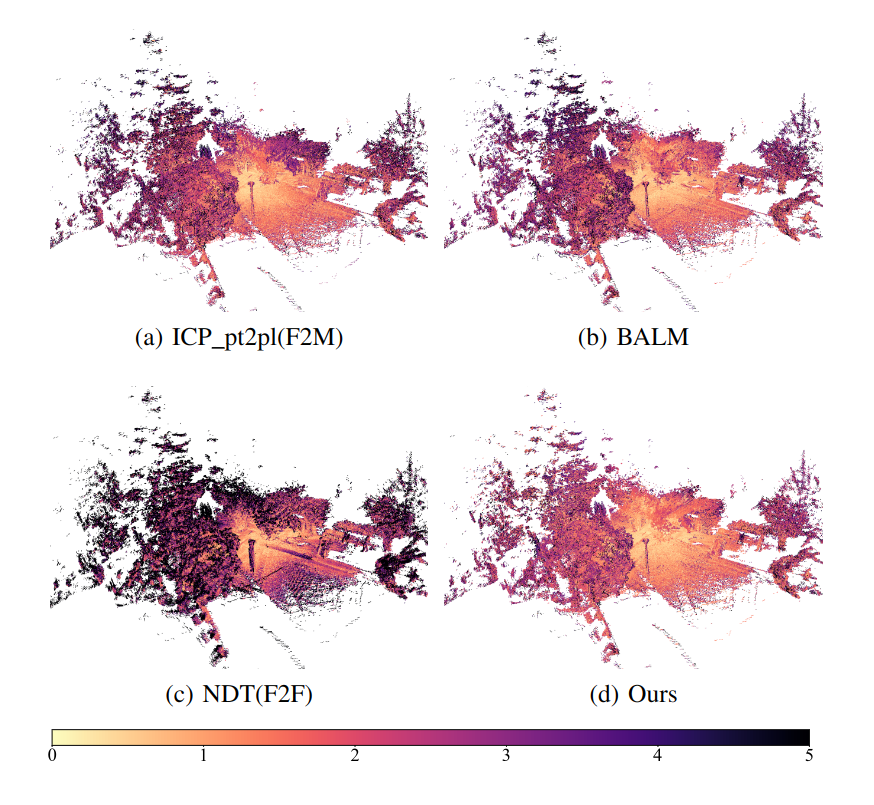
real-world scenarios. The experimental results demonstrate our superiority over the baselines in
terms of both accuracy and speed. Moreover, the results also show that our average positioning
errors achieve the centimeter level.
Method
Least-squares formulation for the objective function.
Frame-wise aggregation of covariance instead of point-wise:
$$\left\{ \begin{aligned} & \boldsymbol{\mu} = \sum_{k} \frac{n_k}{n} \boldsymbol{\mu}_k \\ &
\boldsymbol{\Sigma} = \sum_{k} \frac{n_k}{n} \left( \boldsymbol{\Sigma}_k +
\boldsymbol{\Sigma}_{\boldsymbol{\mu}_k} \right) \end{aligned} \right. ,$$
$$\boldsymbol{\Sigma}_{\boldsymbol{\mu}_k}
= (\boldsymbol{\mu}_k -\boldsymbol{\mu}) (\boldsymbol{\mu}_k -\boldsymbol{\mu})^T.$$
Conditions for optimality of Eigenvalue Minimization (EVM) formulation:
$$\left\{ \begin{aligned} & \mathbf{R}_k \cdot (\mathbf{R}_{\boldsymbol{\Sigma}_k}
\mathbf{e}_{z}) \parallel \hat{\mathbf{n}}, \quad \forall k, \\ & \left( \boldsymbol{\mu}_k -
\boldsymbol{\mu}_{k^\prime} \right) \perp \hat{\mathbf{n}}, \quad \forall
k, k^\prime \end{aligned} \right. ,$$ which can be analogous to aligning the isoplane of each
component.
Results